Recently I have been experimenting with flow-based generative models [1, 2]. These are an interesting class of generative model, with some impressive recent developments [3, 4, 5]), and are probably still somewhat underexplored by the community. In the interests of time I won't explain in detail how these models work here, but in addition to the cited papers there are a couple of good blog posts by Eric Jang providing an overview of flow-based models, and there are some impressive recent results on image modeling (using a model called Glow) on OpenAI's blog. I will highlight again though that some of the notable properties of flow-based models are:

• Exact latent variable inference and likelihood evaluation (in comparison to VAEs and GANs).
• Potentially efficient inference and generation. This is somewhat dependent on architectural choices (if your flow includes an autoregressive model then this is going to slow things down somewhere). However, impressive results are still possible with efficient architectures.

The Glow demos demonstrate the ability to generate realistic images from interpolations of the latent space, and the variations between examples seem somewhat smooth. As I have a background in musical audio modeling, I thought it would be fun to see what sorts of musical sounds could be generated by these models.

Data, model and reconstructed sounds

I selected a subset of around 23000 samples of individual musical instrument sounds from the NSynth Dataset [6], and used them to train a flow-based model that is similar to WaveGlow [5], but uses fixed shuffle layers instead of learned 1x1 convolutions. Like the conditional version of Glow, the model learns a prior that in this case is conditioned on both the input pitch and the instrument type. I don't think that the exact model architecture details matter too much for the purposes of this post (but I might write this up as paper later if people are interested in the finer details). Perhaps more importantly, I used the log magnitude of the (short-time) Fourier transform of the audio as input, similarly to the NSynth baseline model (and also with an FFT size of 1024 and hope size of 256). This was partly because I have quite a lot of experience in working with this representation, but also as I was a bit surprised at the relatively poor performance of basic reconstruction that was reported for the NSynth baseline model. I use Griffin-Lim [7] with 1000 iterations to synthesise a waveform from the spectrograms.

Flow-based models consist of reversible transformations, and so we can do exact reconstruction of the input if desired. An example is given below, along with a CQT plot of the reconstruction (with the original plots taken from [6] for comparison). Notice that the quality of the generation is seemingly much better than the NSynth baseline, but in our case this is trivial, we are really just verifying that Griffin-Lim allows us to generate reasonable reconstructions. The quality remains good even with adding small amounts of Gaussian noise (standard deviation of 0.01) to the inferred latents before generation, so the model is not overly sensitive to the specific inferred value of z.

Original	Wavenet	Baseline

Original	Flow-based model

Exploring the latent space

Exact reconstruction is not particularly interesting, so lets see what happens when we start to move around in the learned latent space. Following the approach [6], I created some reconstructions from linear latent space interpolations (inferring the latent values for two target sounds, then generating a sound from the midpoint between them). This is where we start to run into some issues.

For some combinations of sounds, the generated results are somewhat plausible (and to my ears, more interesting than the NSynth Wavenet equivalent). For example, interpolating between a bass and an organ note:

For others, this doesn't work so well. Half-way between the same organ note and a flugelhorn:

There are some interesting sounds at other intermediate points in the space between these two notes however, as can be heard from a gradual interpolation between the two points (also time-stretched):

To get an understanding of what the model is doing, we can look at one of the generated spectra. This highlights the problem - the model has seemingly just learned to (approximately) linearly interpolate the spectral magnitudes.

Two source inputs, and the spectrum generated from the interpolation in latent space.

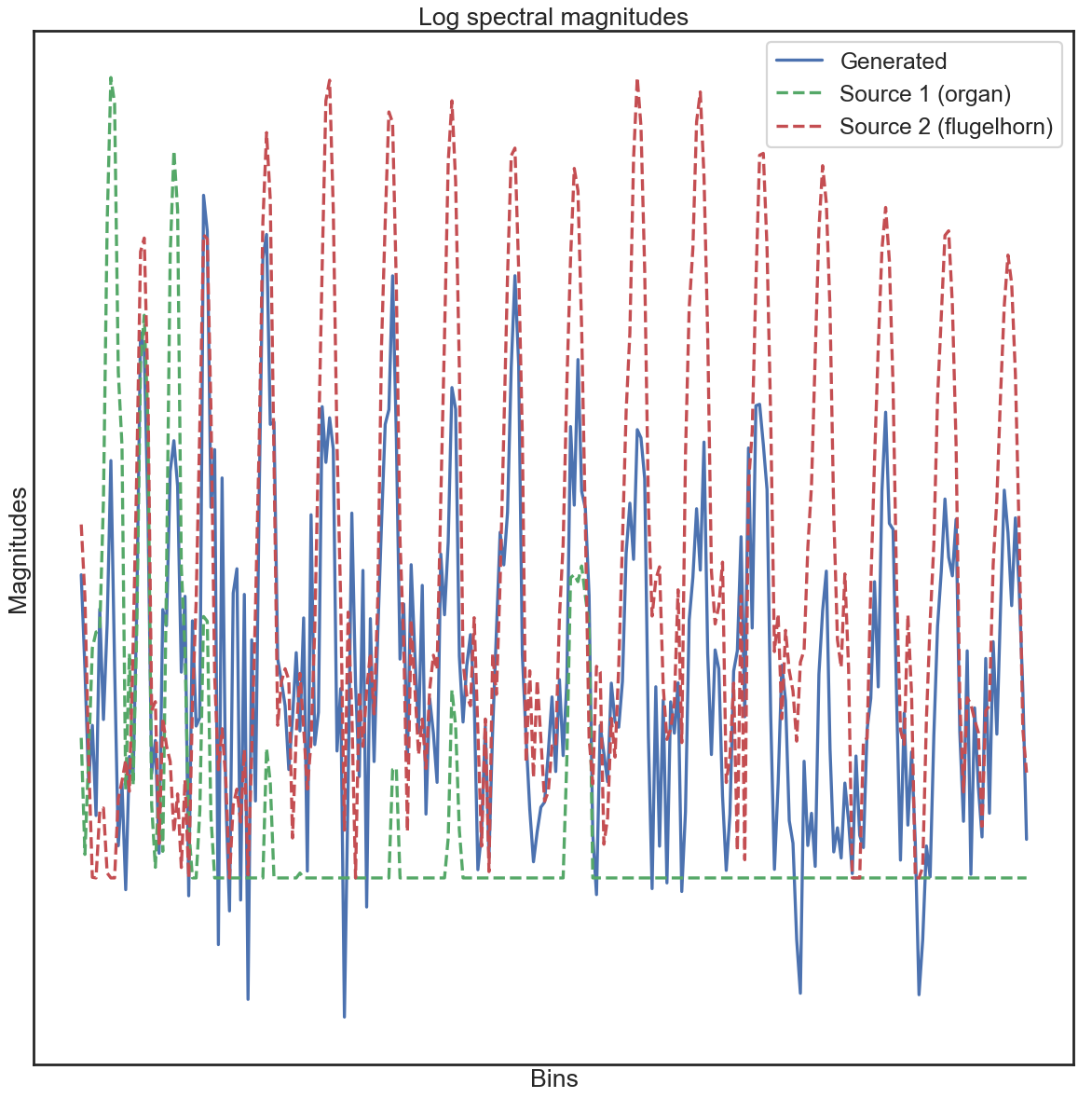
In some ways this is interesting, it was just trained on learning the distribution of existing spectral magnitudes, and has learned a relatively smooth transition (at least from a mathematical perspective). The problem is that this is not necessarily perceptually meaningful. Which is a long-winded way of coming to the central point of this post...

Learning useful representations

What does it actually mean to learn a useful representation?

This question seems to be often glossed over in current literature. It is now quite common to see images generated from latent interpolations, and for particular classes of images (such as faces) it is easy to see why this should work. For other domains such as audio (or natural language, which is the focus of our work at Aylien), results have so far been a bit underwhelming. Some interesting recent models have used other audio input representations such as a Mel spectrogram [5] or the CQT [8]. This is certainly a valid approach, but really I would like the model to learn a useful space itself, rather than having to hardcode a representation in which linear interpolation will works (and possibly change for every task), so ultimately the Wavenet model of reading raw samples and outputting raw samples seems appealing.

Even if we have a specific task in mind at a high-level, in this case perceptually mapping between musical sounds, it is not clear how to frame the learning problem (or encode a loss) so that we learn a representation that is semantically meaningful. Does it actually make sense to talk about learning useful representations in a manner that is divorced from particular downstream tasks?

References